|
Algorytm Euklidesa Ten algorytm jest jednym z najstarszych przepisów - schematów obliczeń. Jest on pomysłowy i szybko daje wynik. Zadaniem jest znalezienie największego wspólnego dzielnika dwóch liczb całkowitych (NWD) - jest to potrzebne na przykład przy skracaniu ułamków. Jak wykonać to zadanie? Pierwszym pomysłem jest sprawdzanie podzielności obu liczb przez kolejne liczby od 2 poczynając, a na mniejszej liczbie kończąc. Można to zrobić na kartce tworząc tabelkę. Przyjrzyjmy się temu sposobowi biorąc liczby 12 i 8:
NWD = 2*2*1=4
Poziom Wynik Opis
-------------------------------------------------------------------------
1 Algorytm Euklidesa - obliczanie NWD dla
dwóch podanych dodatnich liczb całkowitych.
1 12 Podaj pierwszą liczbę: {całkowita, dodatnia}
1 8 Podaj drugą liczbę: {całkowita, dodatnia}
1 Prawda a <> b
1 Prawda a > b
1 4 a := a - b
1 Prawda a <> b
1 Fałsz a > b
1 4 b := b - a
1 Fałsz a <> b
1 4 NWD wynosi:
1 Koniec.
Szybki algorytm Euklidesa polega na braniu reszty z dzielenia większej liczby przez mniejszą zamiast odejmowania. Gdy reszta ta osiągnie zero należy skończyć pętlę i jako wynik wziąć drugą liczbę. Jest on znacznie efektywniejszy od omawianego powyżej. Sprawdźcie to uruchamiając obie wersje algorytmu. |
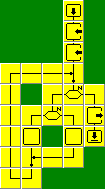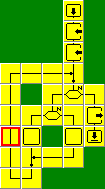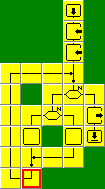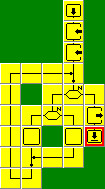 Lepszym i szybszym rozwiązaniem problemu jest
właśnie algorytm Euklidesa. Opiera się on na
fakcie, że jeśli od większej liczby odejmiemy mniejszą, to ta
mniejsza liczba i otrzymana różnica będą miały taki sam
największy wspólny dzielnik jak pierwotne liczby. Gdy przy
kolejnym odejmowaniu otrzymamy parę takich samych liczb, to
znaleźliśmy NWD.
Lepszym i szybszym rozwiązaniem problemu jest
właśnie algorytm Euklidesa. Opiera się on na
fakcie, że jeśli od większej liczby odejmiemy mniejszą, to ta
mniejsza liczba i otrzymana różnica będą miały taki sam
największy wspólny dzielnik jak pierwotne liczby. Gdy przy
kolejnym odejmowaniu otrzymamy parę takich samych liczb, to
znaleźliśmy NWD.